Adesso, invece, vorrei fare un riepilogo cronologico della storia di questi strumenti matematici:
-4000 a.C.: i Sumeri utilizzano i "calculi", piccoli sassolini che permettevano di contare tramite i raggruppamenti e gli spostamenti di questi.
-2000 a.C.: in Cina si sviluppa l'abaco, una semplice tavola ricoperta di polvere o di sabbia e incisa con uno stilo o con le dita per annotare i risultati parziali dei calcoli e i numeri da ricordare; questo strumento è utilizzato anche dai Greci e dai Romani.
-1500 d.C. circa: Leonardo da Vinci inventa uno strano macchinario per effettuare calcoli con il sistema decimale, ma non funziona.
-1550 d.C. circa: Fabrizio Mordente costruisce il compasso "mordente", caratterizzato dalla presenza di cursori con punte ortogonali all'asse delle gambe.
-1597 d.C.: Galileo Galilei inventa il compasso "geometrico e militare", che ha sette linee proporzionali tracciate sulle gambe e quattro scale segnate sul quadrante che consentivano di effettuare operazioni aritmetiche e geometriche.
-1600 d.C. circa: Robert Dudley costruisce un compasso nautico munito di gambe piatte e di visori ed erano impiegati per compiere misurazioni durante la navigazione.
-1617 d.C.: John Napier inventa i "bastoncini" grazie a cui si ottiene la tabellina dei multipli di ogni numero.
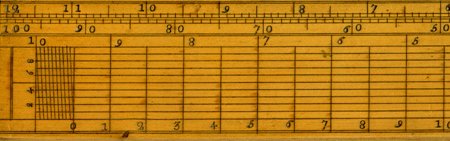
-1620 d.C.: Edmund Gunter inventa il primo regolo calcolatore, dato da una scala logaritmica, dal posizionamento di numeri su un righello e dall'addizione di essi con l'aiuto di un compasso.
-1623 d.C.: Schickard costruisce l' "orologio calcolatore" che era in grado di eseguire somme e sottrazioni grazie ad un sistema di propagazione del riporto con una rotella ad un solo dente.
-1630 d.C.: Edmund Wingate costruisce un regolo calcolatore utilizzando due scale di Gunter, una di fronte all'altra, per eseguire direttamente moltiplicazioni e divisioni, senza l'utilizzo del compasso.
-1632 d.C.: William Oughtred inventa il primo regolo circolare, tracciando due scale di Gunter su cerchi concentrici.
-1642 d.C.: Blaise Pascal inventa la "pascalina", una macchina con cui si poteva sommare e sottrarre e si segnava il riporto.
-1654 d.C.: Robert Bissaker costruì il "Gauging Rule", un regolo specializzato nel misurare il contenuto dei barili di vino, birra o liquori e nel calcolarne il carico fiscale.
-1671 d.C.: Leibniz costruisce la "stepped reckoner", una macchina a scatti con una manovella che permetteva anche di moltiplicare.
-1677 d.C.: Henry Coggeshall creò la "Carpenter's Slide Rule", un regolo che ha permesso di misurare e calcolare il volume e il peso dei carichi di legname.-1709 d.C.: Poleni costruisce una macchina aritmetica che attraverso il meccanismo del "traspositore a denti variabili" riusciva a fare le quattro operazioni elementari.
-1820 d.C.: Thomas de Colmar costruì l’ "aritmometro", un apparecchio portatile commercializzato in grado di eseguire le quattro operazioni, con risultati fino a 12 cifre.
-1823 d.C.: Charles Babbage inventa la "difference engine" che aveva lo scopo di creare tabelle di polinomi utilizzando un metodo numerico chiamato il "metodo delle differenze". Successivamente inventa la "analytical engine", una macchina programmabile per eseguire ogni genere di calcolo utilizzando un sistema di input e output.
-1859 d.C.: Amédée Mannheim costruisce il regolo moderno, migliorando le scale e introducendo il cursore mobile.
-1878 d.C.: George Fuller brevettò l' "Elica Calcolatoria" cilindrica, che servì per progettare dirigibili, aeroplani, ponti e grattacieli.
-1885 d.C.: William Seward Burroughs presentò domanda di brevetto per una macchina addizionatrice dotata della funzionalità di stampa.
-1886 d.C.: Frank Stephen Baldwin costruì una calcolatrice meccanica a tastiera estesa su cui era montato un carello mobile.-1887 d.C.: Felt costruisce il "Comptometer", la prima calcolatrice meccanica dotata di tastiera per l'immissione dei dati e la prima addizionatrice a pressione di tasti.
-1890 d.C.: Hollerith costruisce la "macchina tabulatrice", la prima utilizzata nel campo matematico della statistica e utilizzata dall’amministrazione degli Stati Uniti per sveltire i tempi di rilevazione statistica relativi al censimento della popolazione.
-1936 d.C.: Alan Turing inventa una macchina in grado di eseguire algoritmi e dotata di un nastro infinito su cui può leggere e/o scrivere dei simboli.
Nello stesso anno Zuse intraprese la progettazione e la costruzione dello Z1 che presentava una struttura già molto simile a quella dei moderni computer.
-1948 d.C.: Curt Herzstark costruisce la "curta", prima vera e propria calcolatrice meccanica portatile.
-1961 d.C.: fu lanciata sul mercato la prima calcolatrice totalmente elettronica da ufficio, il Bell Punch/Sumlock ANITA Mk.VII.
-1972 d.C.: vengono usate le prime calcolatrici scientifiche, formate da una fonte di energia elettrica, un display LCD, una memoria e una circuiteria elettronica.
Ora ho definitivamente terminato il lavoro e spero vivamente che questo blog abbia stuzzicato il vostro interesse e soddisfatto la vostra curiosità!